Pi Day 2025
The Question
It's March 14th, or 3/14, or Pi Day, named after the mathematical constant which starts with 3.14 and goes on forever. There's a Pi Day tradition of people competing to memorize as many digits as possible from the never-ending decimal. I got crushed in such a competition last night by Joy (shoutout Joy), and when my coach Ali (shoutout Ali) and I were discussing how to improve my abysmal performance, we started talking about fractions, and arrived at a question: Is there a number of digits of for which it is easier to memorize the fractional approximation than the decimal itself?
The Basics
We decided that for a fraction to be easier to memorize than the decimal it represents, there has to be fewer digits across its numerator and denominator.
Take three-halves.
The fraction here uses 2 total digits across the numerator and denominator (a 3 and a 2) and the decimal uses 2 digits as well (a 1 and a 5). It's no easier to memorize the fraction than the decimal.
But take five-fourths.
2 digits in the fraction, 3 digits in the decimal. You're better off memorizing the fraction - it saves you a digit.
Now, let's see what we can do with .
The Solution
Here's a table with a few common fractions used to approximate (the true value of is provided for reference).
| Value | Decimal Approximation |
|---|---|
| 3.141592653... | |
| 3.142857142... | |
| 3.141509433... | |
| 3.141592920... |
Note that with the first fraction, , there are a total of 3 digits across the numerator and denominator (), and the fraction approximates the decimal version of accurately for 3 digits (). A tie.
For the second fraction, there are a total of 6 digits across the numerator and denominator, and the fraction approximates the decimal version of accurately for 5 digits (). A win for the decimal.
Let's make a new table which captures this.
| Fraction | Decimal Approximation | # of Digits in Fraction | Accurate Digits |
|---|---|---|---|
| 3.142857142... | 3 | 3 (3.14) | |
| 3.141509433... | 6 | 5 (3.1415) | |
| 3.141592920... | 6 | 7 (3.141592) |
We've got our answer! With the 6-digit fraction , you can accurately represent up to 7 digits. Therefore, you'd be better off memorizing the fractional approximation than the decimal.
The Problem with the Solution
Here's the trouble. No Pi Day memorization competition is going to be won by stating just the first 7-digits of the irrational beast. Furthermore, memorizing the fractional approximation is one digit easier than the decimal version? Big whoop. If I wanted to destroy Joy (shoutout Joy) at next year's competition, and flex the might of fractional approximations of , I needed to find a fraction which
- approximates up to hundreds or thousands of digits, and
- is significantly easier to memorize than its decimal counterpart.
The Much Stranger Solution
To find such a fraction, I wrote a Python script to find the least-digit fractional approximation for n-digits of , then graphed the difference in [# of Digits in Fraction] and [# of Digits in Decimal] ("Accurate Digits" column from the table above) for n=0 to n=3000. The result is the following graph.
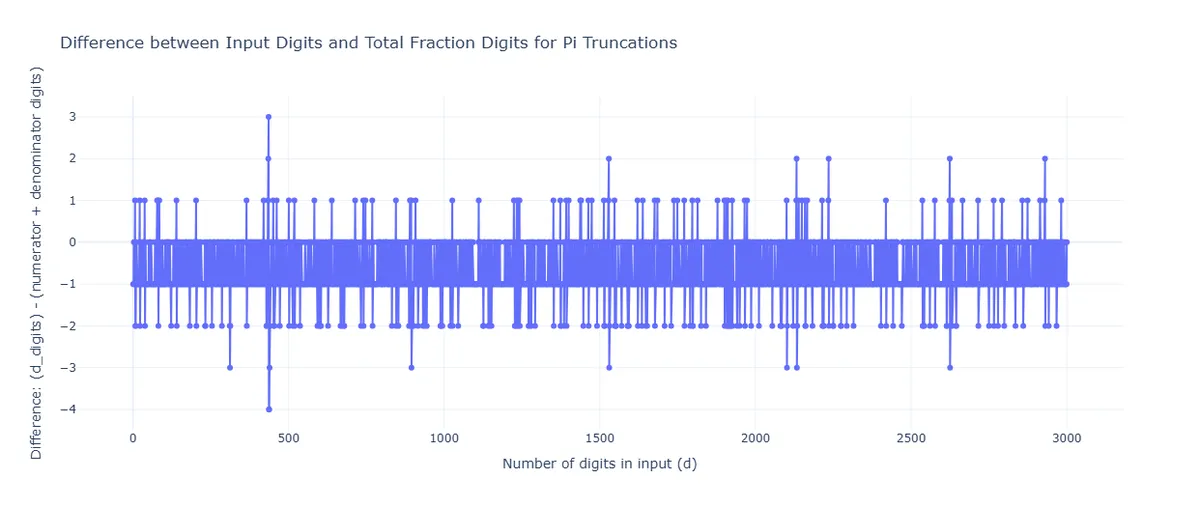
The x-axis is the number of digits of represented (3 is 3.14, 4 is 3.141, and so on). The y-axis is how many digits shorter the fractional approximation is than the decimal representation, where anything above 0 favors the fraction, and below 0 favors the decimal.
For the most part, y-values hover between -1 and 0, indicating it's either slightly easier to memorize the decimal, or there's no difference.
But not for 436!
Let's take a closer look at this meteoric climb and crash just before the 500 digit mark on the x-axis.
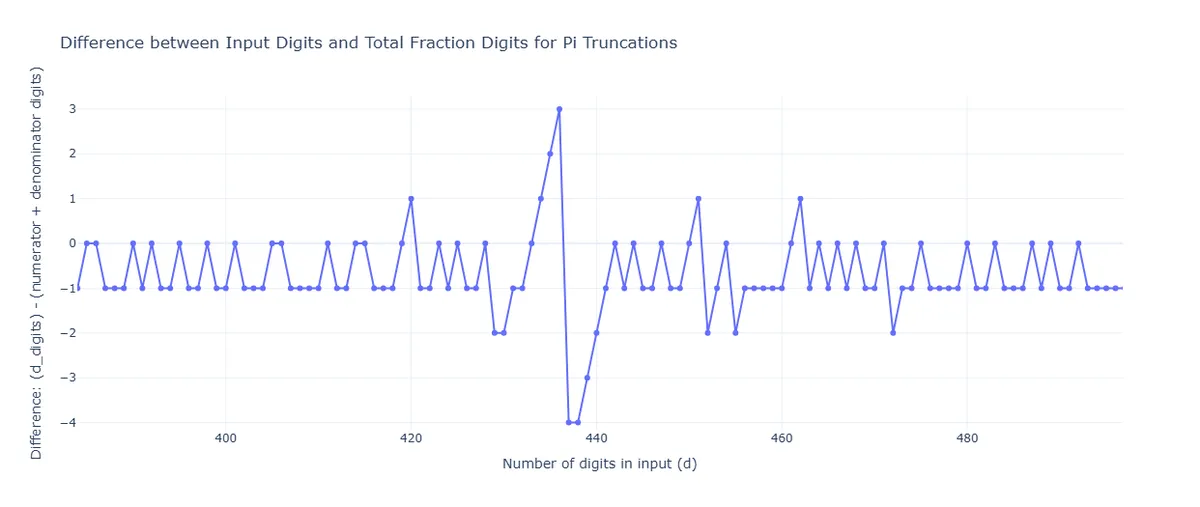
You can accurately represent up to 436 digits with only a 433-digit fraction - a massive win for fractions!
However.
If you slip up.
If you even slightly overshoot 436.
If you step into a Pi Day memorization competition and make the mistake of thinking fractions are the way to go for memorizing 437 or 438 digits of , you will be making an extraordinary mistake.
In order to accurately represent up to 437 digits, a 441-digit fraction is required - an unfathomable loss for fractions.
This is the absolute cliff observed in the graph above. But why? How is it that if you're trying to memorize 436 digits of , you can save yourself 3 digits by memorizing a fraction instead, but if you try to apply this to 437 digits, you'd be hurting yourself to the tune of 4 whole digits? A 7-digit swing?! In this economy?! What is going on?!
I don't know.
Fin.
Appendix
For future Pi Day memorization competitions, instead of memorizing the first 436 digits of in decimal form (3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932), memorize the fraction below. This fraction has 217 digits in the numerator and 216 in the denominator, for a total of 433 digits you need to memorize, saving you 3 digits of trouble. Happy Pi Day!
The fraction:
1901870728566923076090143944714770339621590768313546337192526115562704339680963564320007808107929370299752345187688835741387003036853361285671158059867702399073227994426905220194699766118756059055619036488502928002591
divided by
605384255146420326102361023215940531716391478150345020739231253172134740688232476946000058713774549796561447468267746412874022717544100946587144148739626803435133473281606663121381125761746030151344353855924025288111
Acknowledgments
Thank you Joy for lighting a fire within me which will never burn out. You are the most worthy adversary I've ever faced and your victory over me broke my spirit and led to this piece.
Thank you Ali for texting me back about fractions at 5am after my loss to Joy sent me into a frantic spiral to search for order in this broken world.